マハラノビスの距離に基づく判別係数の求め方
Last modified: Jun 19, 2003
- $k$ 個の群の母集団の平均を $\mathbf{\mu}_{j} = ( \mu_{1j}, \mu_{2j}, \dots , \mu_{pj} )'\ ( j = 1, 2, \dots , k )$,観測値を $\mathbf{X}= ( X_{1}, X_{2}, \dots , X_{p} )'$ とする。
- 各群の分散共分散行列を $\mathbf{\Sigma}_{j}$,その逆行列を $\mathbf{\Sigma}_{j}^{ - 1}$ とするき,$(1)$ 式による各群までのマハラノビス距離を計算し,最も近い群に属すると判定する。
\[
d_j^2 = \left(\mathbf{X}-\mathbf{\mu}_j\right)'\ \mathbf{\Sigma}_j^{-1}\ \left(\mathbf{X}-\mathbf{\mu}_j\right) \tag{1}
\]
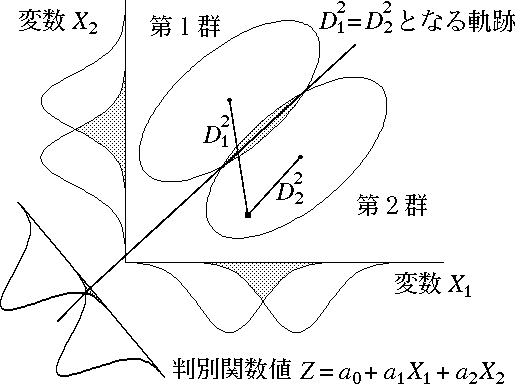 図 1.マハラノビス距離による判別 |
- もし,各群の分散共分散行列が等しい,すなわち $\mathbf{\Sigma}_{1} = \mathbf{\Sigma}_{2} = \dots = \mathbf{\Sigma}_{k} = \mathbf{\Sigma}$ が仮定できれば $(2)$式のようになる。
\[
\begin{align*}
d_j^2 & = \left(\mathbf{X}-\mathbf{\mu}_j\right)'\ \mathbf{\Sigma}^{-1}\ \left(\mathbf{X}-\mathbf{\mu}_j\right)\\
& = \mathbf{X}'\ \mathbf{\Sigma}^{-1}\ \mathbf{X}-2\ \mathbf{X}'\ \mathbf{\Sigma}^{-1}\ \mathbf{\mu}_j+\mathbf{\mu}'_j\ \mathbf{\Sigma}^{-1}\ \mathbf{\mu}_j \tag{2}
\end{align*}
\]
- 第 1 項は各群に共通,第 3 項は各群ごとに異なる定数( これを $c_{j}$ とする )である。各ケースごとに異なるのは第 2 項のみであるから,$(3)$ 式の計算を行えばよい。
\[
-2\ \mathbf{X}'\ \mathbf{\Sigma}^{-1}\ \mathbf{\mu}_j = a_{1j}\ X_1 + a_{2j}\ X_2 + \dots + a_{pj}\ X_p \tag{3}
\]
- 係数 $a_{1j}, a_{2j}, \dots , a_{pj}$ は $\mathbf{\Sigma}^{ - 1}$ の要素を $\sigma^{ij}$ とすれば $(4)$ 式で求められる。
\[
a_{ij} = -2\ \left(\ \sigma^{i1}\mu_{1j} + \sigma^{i2}\mu_{2j} + \dots + \sigma^{ip}\mu_{pj}\ \right),\ \ \ i=1, 2, \dots, p \tag{4}
\]
- $(2)$ 式の第 1 項は群に関係ないため無視できるので,$(5)$ 式の数値が最も小さい群に属すると判定すればよい。$(5)$ 式は,分類関数と呼ばれる。
\[
f_j = a_{1j}\,X_1 + a_{2j}\,X_2 + \dots + a_{pj}\,X_p + c_j \tag{5}
\]
- また,マハラノビス距離の大小を比較する代わりにあらゆる $2$ 群の組合わせに対して,$(6)$ 式で表される ${}_{k}C_{2}$ 個の判別関数を定義しておくこともできる。例えば,第 $1$ 群と第 $2$ 群の判別関数は,
\[
\begin{align*}
Z_{1\cdot 2} &= d_1^2 + d_2^2 \\
&= (a_{11}-a_{12})\,X_1 + (a_{21}-a_{22})\,X_2 + \dots + (a_{p1}-a_{p2})\,X_1 + (c_1-c_2) \tag{6}
\end{align*}
\]
- $(6)$ 式の判別関数は群の数が $2$ 群のときは $1$ 個の判別関数を計算すればよいので便利であるが,群の数が $3$ 群以上のときには,やや煩わしい。
- 判別方法としてはこの他に,$(2)$ 式の $d_{j}^{2}$ が自由度 $p$ の $\chi^2$ 分布に従うことを利用する方法がある。各群の中心からのマハラノビス距離から $P = \Pr \{ \chi^2 \geqq d_{j}^{2} \}$ を求め,$P$ の最も大きい群に所属すると判別する。これは,$d_{j}^{2}$ 値の最も小さい群に所属すると判別することと同じであり,わざわざ各群へ所属する確率を求める必要はなさそうに思うかもしれないが,どの群にも所属しないケースの可能性を考えるとこのような方法をとる必要性がわかるであろう。
- なお,各群の分散共分散行列が等しくない場合は,判別境界は,図 1 のような直線ではなく,図 2 のような二次曲線になるので,$(1)$ 式による判別は二次の判別関数と呼ばれる。
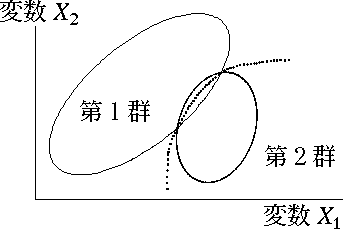 図 2.二次の判別関数 |
2 群の判別の場合
2 群の判別の場合,計算は若干簡単になる(計算例)。
- 各群の変動・共変動行列を $\mathbf{S}^{ ( 1 ) }$,$\mathbf{S}^{ ( 2 ) }$,$2$ 群をプールしたときの分散・共分散行列を $\mathbf{V}$ とすると,それぞれの要素は以下のように定義される。
\[
\left \{
\begin{eqnarray}
S_{ij}^{(1)} &=& \sum_{m=1}^{n_1} \left( X_{im1}-\bar{X}_{i1} \right) \left( X_{jm1}-\bar{X}_{j1} \right) \\
S_{ij}^{(2)} &=& \sum_{m=1}^{n_2} \left( X_{im2}-\bar{X}_{i2} \right) \left( X_{jm2}-\bar{X}_{j2} \right) \\
V_{ij} &=& \frac{S_{ij}^{(1)} + S_{ij}^{(2)}} {n_1+n_2-2}
\end{eqnarray}
\right .
\]
- また,各変数の平均値の差のベクトル $\mathbf{d}$ を,
\[
\mathbf{d} =\left( \bar{X}_{11}-\bar{X}_{12},\ \bar{X}_{21}-\bar{X}_{22},\ \dots,\ \bar{X}_{p1}-\bar{X}_{p2}\ \right)'
\]
とすると,$\mathbf{a}$ は以下の連立方程式を解けば得られる。
\[
\left \{
\begin{eqnarray}
a_1\,V_{11} + a_2\,V_{12} + \dots + a_p\,V_{1p} = d_1 \\
a_1\,V_{21} + a_2\,V_{22} + \dots + a_p\,V_{2p} = d_2 \\
\vdots \\
a_1\,V_{p1} + a_2\,V_{p2} + \dots + a_p\,V_{pp} = d_p \\
\end{eqnarray}
\right .
\]
- 行列で表せば,$\mathbf{V\ a} = \mathbf{d}$ ゆえ,$\mathbf{V}$ の逆行列を $\mathbf{V}^{ - 1}$ とすれば,$\mathbf{a} = \mathbf{V}^{ - 1}\ \mathbf{d}$ である。
演習問題:
応用問題:
 次のページへ進む
次のページへ進む
 判別分析の最初のページへ戻る
判別分析の最初のページへ戻る
 E-mail to Shigenobu AOKI
E-mail to Shigenobu AOKI


