No.15896 Re: クラスカル・ウォリス検定 【青木繁伸】 2011/12/07(Wed) 19:36
> クラスカル・ウォリス検定は検定をするデータの中央値に差があるかどうかを調べるものですか?
> それともそのデータにつけた順位の中央値に差があるかと言うものですか?
衝撃的かも知れませんが,どちらでもないです。
> set.seed(12345)見て分かるとおり,同じにはなりません。(一元配置分散分析なら,平均値の同じ3群なら,p 値は 1 になる)
> # x,y,z の 3 群のデータ
> # z2 は z の大きい方から 4 つに下駄をはかせたもの
> x <- sort(sample(20:90, 10))
> y <- sort(sample(20:90, 10)+15)
> z <- sort(sample(20:90, 10)+30)
> z2 <- ifelse(z > 93, z+20, z)
> cbind(x, y, z, z2)
x y z z2
[1,] 30 35 64 64
[2,] 41 37 72 72
[3,] 50 45 75 75
[4,] 52 46 80 80
[5,] 65 60 82 82
[6,] 71 61 84 84
[7,] 72 65 93 93
[8,] 80 85 95 115
[9,] 81 94 98 118
[10,] 89 99 116 136
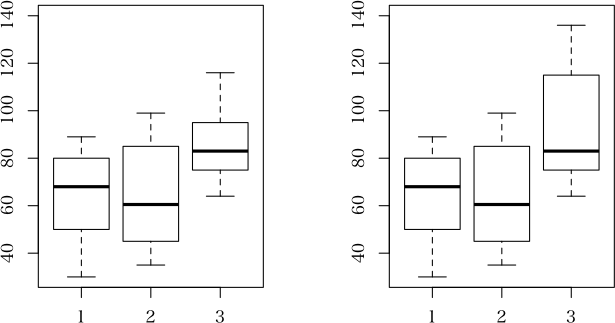
> layout(matrix(1:2, 1))
> boxplot(v~g, ylim=c(30, 140))
> boxplot(v2~g, ylim=c(30, 140))
> layout(1)
> # v=(x, y, z) と v2=(x, y, z2) のデータセットを考える
> v <- c(x, y, z)
> v2 <- c(x, y, z2)
> # 元データの中央値は v でも v2 でも同じ
> tapply(v, g, median)
1 2 3
68.0 60.5 83.0
> tapply(v2, g, median)
1 2 3
68.0 60.5 83.0
> # 順位の中央値も v でも v2 でも同じ
> tapply(rank(v), g, median)
1 2 3
13.25 9.50 21.50
> tapply(rank(v2), g, median)
1 2 3
13.25 9.50 21.50
> # ならば,クラスカル・ウォリスの検定も同じになるか?
> g <- as.factor(rep(1:3, each=10))
> kruskal.test(v~g)
Kruskal-Wallis rank sum test
data: v by g
Kruskal-Wallis chi-squared = 6.973, df = 2, p-value = 0.03061
> kruskal.test(v2~g)
Kruskal-Wallis rank sum test
data: v2 by g
Kruskal-Wallis chi-squared = 7.4456, df = 2, p-value = 0.02417
同じにならない原因はグループごとの順位和が違うから
> tapply(rank(v), g, sum)正確に言えば,平均順位の差を見ている。つまり,順位をデータだと思って一元配置分散分析することに対応する(意味的に対応するだけで,結果が同じになるわけではない)。
1 2 3
124.5 125.5 215.0
> tapply(rank(v2), g, sum)
1 2 3
124.5 123.5 217.0