No.16724 Re: 前回のロジスティック重回帰分析と単回帰分析の現象と証明 【青木繁伸】 2012/04/05(Thu) 15:44
話が複雑そうだったので,敬遠しておりましたが,以下のようなことでしょうか?
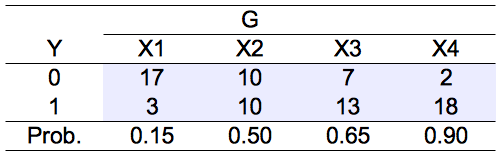
1. データは,添付図のように,X1〜X4 の4群で,目的変数は二値変数。つまり,X1 群の 20 例では 15%,X2 群の 20 例中では 50%,X3 群の 20 例中では 65%,X4 群の 20 例中では 90% が陽性(ある質問に「はい」と答えるなど)。
2. 4群をダミー変数3個で表して説明変数として,目的変数をロジスティック回帰する。
3. 2.で基準とした群とその他の1群の計2群を取り出して,群を表すダミー変数1個を説明変数として,目的変数をロジスティック回帰する。3通りの分析がある。
4. 2.の結果と3.の結果は同じになる。
そういうことでしたら,その通り。以下に説明しましょう。
まず,SPSS のロジスティック回帰と R のロジスティック回帰で,カテゴリー変数のどのカテゴリーを基準とするかが違のですが(SPSS は最後のカテゴリー,R は最初のカテゴリー),それは本質な問題でないので,R で説明します。
最初に,X1 と X2 群を取り上げてロジスティック回帰することを考えます。
ロジスティックモデルは
最終的には,
を解くということで,
です。R で解くと,
> d12 <- d[d[,2] == "X1" | d[,2] == "X2",]となります。X1 と X3,X1 と X4 についても同じようになります。
> ans.12 <- glm(Y~G, d12, family=binomial)
> summary(ans.12)
:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.7346 0.6262 -2.770 0.00561 **
GX2 1.1156 0.7823 1.426 0.15385
最後に,X1 〜 X4 全部を使って回帰分析することを考えます。目的変数の取る値は,0.15,0.35,0.65,0.90 の4つです。回帰式は
これを見れば分かりますが,
な ぜこんなことになるかといえば,どの群に属するかという情報だけを使ってロジスティック回帰をするということは,ある群の予測値としては,その群の標本比 率が一番よい(最尤推定)であるということです。しかし同時にそれは,最もシンプルで馬鹿馬鹿しい(?)結果に過ぎないということです。
単純に重回帰分析を使って予測する場合も同じようになります。