「統計学関連なんでもあり」の過去ログ--- 045

No.17142　ロジスティック回帰　　【まる】　2012/07/04(Wed) 23:22

初めて投稿させていただきます．
勉強不足な面が多々あるかと思いますが，どうかご容赦下さい．

ある論文で，生物の体長を独立変数，巣を持つか持たないかを説明変数としてロジスティック回帰分析を行っていました．
その結果有意差がみられ，より大きな個体の方がより巣を持ちやすい傾向にあると結論づけられていました．

しかしながらこの場合，巣を持つグループと持たないグループで平均値の差の検定を行うものではないかと疑問に思ってしまいました．
また，図を見る限り，平均値の差の検定ではとても有意差がでないデータという印象を持ちました．
もし本当に平均値の差の検定で有意差がなければ，「巣を持つグループと持たないグループに体長差はないが，より体長の大きな個体のほうが巣を持ちやすい傾向にある」という解釈になり，若干矛盾を感じます．

そこで質問なのですが，サンプル数が少ない，あるいはばらつきが大きくて平均値の差の検定で有意差が出なかった場合，ロジスティック回帰分析を行って傾向のみを述べるという方法は正しいのでしょうか？

また，ひとつの連続型データとひとつのカテゴリカルデータを用いて，ロジスティック回帰分析を行うプロセスが載っている参考ページがあれば是非教えて下さい．
よろしくお願い致します．

No.17144　Re: ロジスティック回帰　　【青木繁伸】　2012/07/05(Thu) 08:37

> 生物の体長を独立変数，巣を持つか持たないかを説明変数としてロジスティック回帰分析

巣を持つか持たないかは「被説明変数（従属変数）」ですね。

> 図を見る限り，平均値の差の検定ではとても有意差がでないデータという印象

印象とは不正確なものです。少なくとも，統計学的に有意な場合でも，図にすると有意ではないように見えるということは数多くあります（二群の平均値±1.96×SE を描いた図なんかは特に）。

> サンプル数が少ない，あるいはばらつきが大きくて平均値の差の検定で有意差が出なかった場合，ロジスティック回帰分析を行って傾向のみを述べるという方法は正しいのでしょうか？

別に誤ってはいないでしょう。傾向をいうなら平均値±1.96×SEを表示するだけで充分でしょう。それに追加してロジスティック回帰分析を行えば，それに追加される情報が得られるでしょう。

No.17145　Re: ロジスティック回帰　　【青木繁伸】　2012/07/05(Thu) 10:39

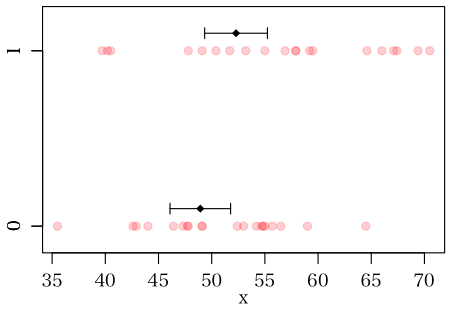
図を見て，二群の平均値に差があるかないか，わかるでしょうか?2つのエラーバーはそれぞれ，平均値±1.96SE で描かれています（わざと，検定結果がギリギリの状況になるようにデータを作ってあります）。

平均値は，50.61 と 56.20 です。

平均値の差の検定（ウェルチの方法）の結果は，P値 = 0.04066 です。ギリギリ有意です。

ロジスティック回帰分析の結果は，
            Estimate Std. Error z value Pr(>|z|)  
(Intercept) -4.47356    2.29390  -1.950   0.0512 .
x            0.08382    0.04257   1.969   0.0490 *
となりました。

やはり，x の回帰係数は有意であるということになりました。

平均値の差の検定に加わった情報は，偏回帰係数が 0.08382 であるということです。また予測値（予測確率）を計算することもできるようになりました。

No.17146　Re: ロジスティック回帰　　【まる】　2012/07/05(Thu) 11:09

青木先生

大変丁寧な解説をありがとうございました．
例題まで示してくださったおかげで，自分の思い込みによる勝手な判断がいかに危険であるかを思い知らされました．
私の専門分野ではあまり見ない方法だったのですが，今後自分の研究にも応用していきたいと思います．