No.17218 Re: グループごとオッズ比と全体オッズ比の違い 【raraki】 2012/07/20(Fri) 15:41
シンプソンのパラドックスをキーワードにして検索をかけてみるとよいかと思います。
No.17219 Re: グループごとオッズ比と全体オッズ比の違い 【青木繁伸】 2012/07/20(Fri) 16:24
シンプソンのパラドックスですね
必要な結果を纏めて表示しておきます
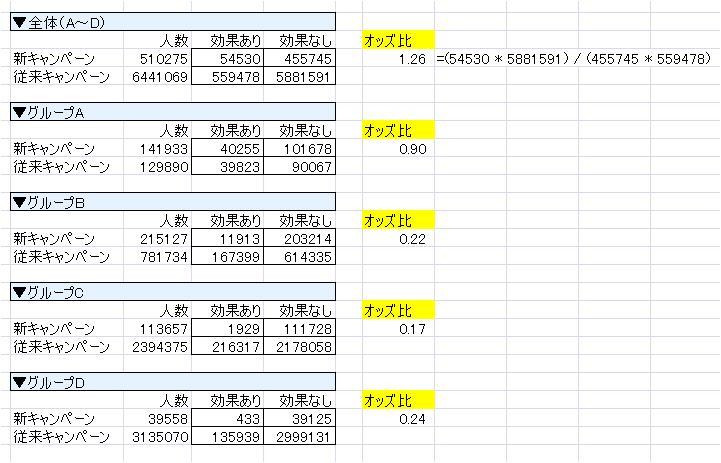
A+B+C+D について
新キャンペーン( 7.3%),効果あり10.7%, 効果無し89.3%
従来キャンペーン(92.7%),効果あり 8.7%, 効果無し91.3%
オッズ比=1.258
A について
新キャンペーン(52.2%),効果あり28.4%, 効果無し71.6%
従来キャンペーン(47.8%),効果あり30.7%, 効果無し69.3%
オッズ比=0.895
B について
新キャンペーン(21.6%),効果あり 5.5%, 効果無し94.5%
従来キャンペーン(78.4%),効果あり21.4%, 効果無し78.6%
オッズ比=0.215
C について
新キャンペーン( 4.5%),効果あり 1.7%, 効果無し98.3%
従来キャンペーン(95.5%),効果あり 9.0%, 効果無し91.0%
オッズ比=0.174
D について
新キャンペーン( 1.2%),効果あり 1.1%, 効果無し98.9%
従来キャンペーン(98.8%),効果あり 4.3%, 効果無し95.7%
オッズ比=0.244
新キャンペーンと従来キャンペーンへ割り振られた例数の割合が,A と (B, C, D) で逆になっているのが主たる原因です。そして,(B, C, D) は A に比べて合計例数が大きい。
A, B, C, D を合計した表で,新キャンペーンで効果ありは 54530 だが,そのうちの 40255(73.8%)が A 由来。そして,A は新キャンペーンの方が従来キャンペーンより効果ありということ。B, C, D は従来キャンペーンに割り振られた例数がおおく,そちらの方が効果ありとするものが多い。
結果の傾向が同じでも,下位集団の割合が逆になっている場合には,集計表を単純に足し併せると,結果は薄まったり,逆方向になったりということになります。
A と D を足したものについて考察するとよりはっきりするでしょう。
A+D について
新キャンペーン( 5.3%),効果あり22.4%, 効果無し77.6%
従来キャンペーン(94.7%),効果あり 5.4%, 効果無し94.6%
オッズ比=5.079
No.17231 Re: グループごとオッズ比と全体オッズ比の違い 【波音】 2012/07/22(Sun) 10:36
rarakiさん,青木先生
ご回答ありがとうございます。
(早速のお返事,たいへん助かりました!)
相関係数でよくある,性別という変数を考慮して男女別に相関係数をみると,男女混みで見た場合との相関と異なるというのも「シンプソンのパラドックス」だったのですね。分割表でも同じようなことがあるのは,今回,はじめて問題に直面しました。
シンプソンのパラドックスについて調べてみると,分割表の解析で知らないことがけっこうたくさんあることに気づかされました(^_^;)
● 「統計学関連なんでもあり」の過去ログ--- 045 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る