[1]TRUE
$parameters
[1] 319491448 -404587515 134213440 -31694816
[1]514.5493
(別の実行では。。。)
$parameters
[1]161.14218 -100.83851 72.65116 -1948.57888
$residuals
[1] 514.5493
(別の実行では。。。)
[1] 161.14218 -100.83851 72.65116 -1948.57888
$residuals
[1] 808.6103
「初期値を乱数で決めているから,誤差範囲ないで少し違います」とHPにありますが,少しでないような気がします。
http://aoki2.si.gunma-u.ac.jp/R/simplex.html
やり方が間違っているのか,それともこの程度の違いは許容範囲なのでしょうか?
長くなってなってしまいましたが,近くでRを使用している人がおらず,恐れ入りますが,ご回答よろしくお願いします。
x y
1970 36.820738
1971 31.082227
1972 28.474470
1973 27.355919
1974 21.683815
1975 18.131384
1976 14.262826
1977 9.311827
1978 7.575328
1979 2.811892
1980 2.632602
1981 -0.718945
1982 -4.656446
1983 -4.820679
1984 -8.509212
1985 -10.449176
1986 -13.955607
1987 -17.161785
1988 -17.464104
1989 -19.961663
1990 -20.249097
1991 -23.243893
1992 -22.504964
1993 -24.640356
1994 -26.486722
1995 -23.101160
1996 -31.833200
1997 -34.244073
1998 -31.364166
1999 -33.169396
2000 -38.214761
No.17311 Re: 関数のあてはめ 【青木繁伸】 2012/08/18(Sat) 06:34
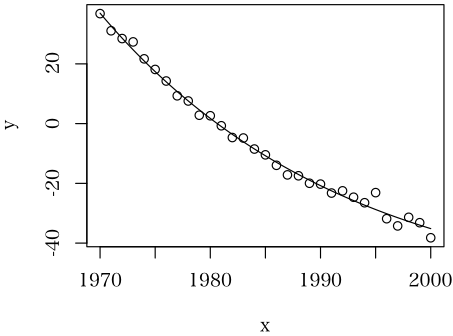
simplex 法での当てはめにおいて,plot.flag=TRUE を指定してあるので,当てはめ結果の図が表示されたと思いますが,それを見てどう思いましたか?
何通りかの答えが出ても,見た目は同じような曲線(直線に近いが)が表示されたと思いますが?
x=1970〜2000 の範囲で,得られたパラメータの推定値で 横軸を x,縦軸に exp((x+a4)/a3) を描くと,どのような場合でもほとんど直線になります。相関係数を求めるとほとんど 1 ということになりますね。従って実際には y = a1+a2*x の直線回帰をしているのとほとんど同じになります。この観点からいえば,「この程度の違いは【このモデル式を採用する限りは】許容範囲」ということになる でしょう。
a1〜a4 のパラメータ全部を使ってあてはめをした場合には,わずかに「上に凸」の曲線になりますね。しかし,実際のデータは「下に凸」のようです。これではちゃん と当てはまる(パラメータが妥当に推定できる)ということはないでしょう。なぜこのモデル式が出てきたのか分かりませんが,もしデータに合うような任意の 曲線でよければ,下に凸であるモデル式を探索した方がよいでしょう。例えば,以下のような曲線によくフィットします。ans <- nls(y~a*b^(x-1970)+c, data=d, start=list(a=1, b=0.9,c=1))
x2 <- seq(1970, 2000, length=100)
nd <- data.frame(x=x2)
y2 <- predict(ans, nd)
plot(d)
lines(x2, y2)
No.17316 Re: 関数のあてはめ 【マッカラン】 2012/08/18(Sat) 12:23
ご回答,ありがとうございました。
確かに当てはめた結果の図はほぼ同じでした。若干,凸の度合いが違うときもありましたが。
あと,どうしてこの関数を当てはめようとしたかですが,これは死亡率予測モデルの一種で,yは死亡率の改善度を表しています。
(いわゆるLee-Carterモデルのktです)
平均寿命は今後も改善していくという考えと,改善は穏やかになるという考えがあるため,指数関数と対数関数を当てはめて,その和半で将来の死亡率を予想しようとするモデルです。
対数関数の当てはめは"nls"で求めることができたので,今回の書き込みでは省略しておりました。
ただし,データをみると明らかな下に凸なので,モデルどおり和半するのがいいのかも含めて,もう少し検討してみます。
ありがとうございました。
● 「統計学関連なんでもあり」の過去ログ--- 045 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る