No.20165　二回のデータ変換　　【ぼぶ】　2013/08/27(Tue) 23:58

データの変換を2度実行することは確かな結果を得るために許されるのでしょうか。

統計学初心者です。
現在SPSSを使って回帰分析（最小二乗法）を行い，レポートを書いています。
GDPが従属変数です。
GDPの分布が極度に正であったため，1で割ってinverseに変換したところ，適度に正になりました。
そこで，GDPのinverseをSQRTに変換したところ，綺麗な正規分布になりました。
その他の仮定もクリアしたため，このまま回帰分析を行いたいのですが，2回データ変換を行い回帰分析を行うことはありえますか？
論文などでそういった従属変数を見たことがないので，詳しい方がいらっしゃいましたらご教示ください。

下記統計学に関するウェブサイトのガイダンスに沿って変換しました。(https://statistics.laerd.com/premium/t/transformations-in-spss.php)

注：英語版SPSS，レポートのため日本語訳が間違っているかもしれません。ご了承ください。
よろしくお願いいたします。
No.20166　Re: 二回のデータ変換　　【青木繁伸】　2013/08/28(Wed) 07:07

「分布が極度に正」とは，「歪度が正」ということでしょうか？

回帰分析においては，独立変数，従属変数とも，「正規分布に従わなければならない」という呪縛はないはず。

URL は，ログインを要求されるようで，内容が確認出来ません。

単に書き間違いの「1で（を）割ってinverse後，平方根をとる」は，従属変数の「-1/2乗，-0.5乗」ということなので，別に二段階変数変換ではないでしょうし。

ただ，どんな変数変換をしてもよいというのではなく，その背景には理論が必要とは思います。変数の -0.5 乗して正規分布になるのはべき乗分布ですね。べき乗分布の場合はたとえば，
y^α=x1^β * x2^γ * …xp^ω
というのが母回帰（変な回帰式と思うかも知れませんが，経済学の分野ではよく使われる）なら，両辺の対数を取ってαで割れば
log(y)={βlog(x1) + γlog(x2) + … + ωlog(xp) } / α
で，log(y), log(x1), log(x2), ..., log(xp) を使えば重回帰分析になりますけどね。

従属変数が二項分布（多項分布）やポアソン分布や負の二項分布など正規分布以外に従う場合には，それなりの方法（glm）を使いますけど。
No.20167　Re: 二回のデータ変換　　【ぼぶ】　2013/08/28(Wed) 09:02

早速のお返事ありがとうございます。
はい，歪度が正ということです。
申し訳ありません，書き忘れてしまいましたが，重回帰分析です。
また，例のウェブサイトの説明を読み間違えていました。
「も し従属変数と独立変数，または独立変数同士が直線関係でない場合は，データの変換（transform）が必要である」とあり，そこから変換の手順のペー ジに飛ぶと「正規分布にしたい場合はデータの変換が必要である」というような言い方から変換の手順が始まっています。
とにかく，青木様の仰るとおり重回帰分析をする際従属変数が正規分布に従う必要はないのですね。

私が混同してしまい間違った説明をしてしまっていました。
（正規分布ではなく）誤差の不偏性と等分散性を満たすために従属変数の変換が必要で，そのために正規分布にしたがっているかどうかを確認し，「歪度が極度に正」であることがわかりました。
そのサイトには，
「歪度が適度に（moderately）正」のデータにはsquare root
「歪度が強く（strongly）正」のデータにはlogarithm
「歪度が極度に（extremely）正」のデータにはinverse
とありました。
（念のためその説明の部分のスクリーンショットを添付させていただきます。）
な ので，inverseにしたところ，歪度が適度に正になったため，square rootにしたところ綺麗な正規分布になり，その他の仮定（誤差の不偏性，等分散性など）もすべて満たし，重回帰分析の結果も有意で満足するものになりま したが，これではデータを変換しすぎなのではないか？と思い質問させていただいた次第です。しかしながらここまで来るのにかなり時間をかけてきて最初から やり直す時間もないので，もし完全に間違いでないのならばこのデータ使いたい所存です。

勉強不足で，理論は理解しておらず，上記説明通りやってしまっていました。
申し訳ありません，青木様の説明してくださったことを完全に理解できていないのですが，従属変数が正規分布以外に従う場合には"GDP_inverse_sqrt"を従属変数として最小二乗法を利用するのではなくその他の方法を用いるべき，ということでしょうか。
長くなってしまいましたが，何卒よろしくお願いいたします。

No.20168　Re: 二回のデータ変換　　【青木繁伸】　2013/08/28(Wed) 10:06

> そのサイトには，
> 「歪度が適度に（moderately）正」のデータにはsquare root
> 「歪度が強く（strongly）正」のデータにはlogarithm
> 「歪度が極度に（extremely）正」のデータにはinverse
> とありました

試行錯誤的にやるのではなく，ボックス-コックス変換をやれば，どのような変数変換が有効なのか，客観的に分かります。

-0.5 乗なので別に2段階の変数変換をしているわけではありませんといいました。

それで，重回帰すればよいでしょう。

理論的な裏付けがある方がよいでしょうねということ。-0.5 乗したものが線形回帰式で表現できるという，経済学上の理論があればなんの問題もないでしょう。なくても，とにかく説明できればということなら，それはそれで。
No.20171　Re: 二回のデータ変換　　【青木繁伸】　2013/08/28(Wed) 11:33

ところで，GDP ですが，ある国の時系列データではなくて世界の国々のデータということでしょうかね？

http://www.env.go.jp/doc/toukei/data/2013_1.36.xls

にあるような。

あなたのデータで，歪度を計算してみたら「極度に正」だったというだけですか？

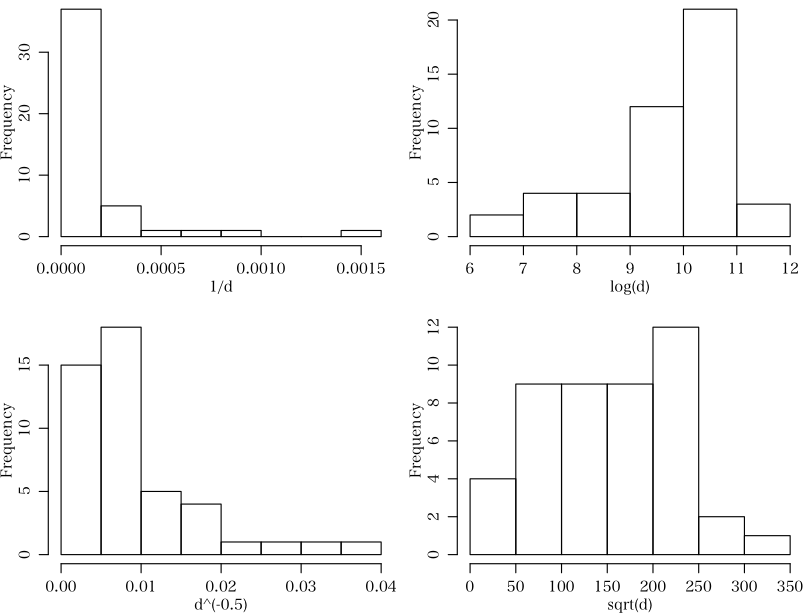
ヒストグラム描いてみましたか？総務省からのデータでは，このデータは，平方根変換もしくは対数変換するのが一番良さそうですね。

2010 年 1 人当たり GDP
42983, 1406, 2949, 21052, 15836, 43783, 4613, 4354, 10095,
1003, 670, 2140, 31824, 8373, 46546, 46361, 9101, 9162, 10716,
39278, 46220, 36327, 33877, 45159, 46910, 26504, 68880, 48906,
30543, 18839, 55830, 39857, 84589, 12884, 44502, 39546, 43815,
12263, 21438, 105095, 10351, 2654, 4222, 7255, 57119, 32372
> skew(d)
[1] 0.9602841
> skew(1/d)
[1] 3.480694
> skew(d^(-0.5))
[1] 2.184312
> skew(d^0.5) # = skew(sqrt(d))
[1] 0.03075878
> skew(sqrt(d))
[1] 0.03075878
> skew(log(d))
[1] -0.9245506

No.20188　Re: 二回のデータ変換　　【ぼぶ】　2013/09/02(Mon) 17:56

青木様，無事解決致しました。ご丁寧にお応えいただきありがとうございました

● 「統計学関連なんでもあり」の過去ログ--- 046 の目次へジャンプ
● 「統計学関連なんでもあり」の目次へジャンプ
● 直前のページへ戻る