「統計学関連なんでもあり」の過去ログ--- 046

No.20393　従属変数について　　【推計初心者】　2013/11/01(Fri) 20:48

今統計ソフトstataを使って推計をしようとしているところなのですが，従属変数に全要素生産性（TFP）を置いていて，それがマイナスになっている産業があって，自然対数が取れないです。こういう場合はどうすればよろしいでしょうか？
自然対数をとらずに，説明変数のみ自然変数をとって推計を行うのですか？

No.20395　Re: 従属変数について　　【青木繁伸】　2013/11/01(Fri) 21:19

> 従属変数に全要素生産性（TFP）を置いていて，それがマイナスになっている産業があって，自然対数が取れないです。...説明変数のみ自然変数をとって

ということは，y = α * x^β * z^γ * … * ε　というようなモデルですかね？
先行研究でどのようにしているかが参考になるのでは？

対数がとれないというか，対数なんかとらずに非線形回帰すればよいのではないかと思いますけど。

No.20397　Re: 従属変数について　　【推計初心者】　2013/11/01(Fri) 21:53

>ということは，y = α * x^β * z^γ * … * ε　というようなモデルですかね？
先行研究でどのようにしているかが参考になるのでは？
対数がとれないというか，対数なんかとらずに非線形回帰すればよいのではないかと思いますけど。

返事ありがとうございました。
先ほどの質問に続くですが，被説明変数に自然対数をとらないで，説明変数のみ取ればよいということなのですか，
また，被説明変数に自然対数をとらないのと取るのと推計方法は変わりますか？

No.20398　Re: 従属変数について　　【青木繁伸】　2013/11/01(Fri) 22:11

あなたが使おうとしているのは，どのようなモデルですか？
y = α * x^β * z^γ * … * εであるならば，両辺の対数をとって log y = log α + β log x + γ log z + …　のようになるので，重回帰分析に帰結するというのが，旧来（旧式）の解析法でしょう。教科書にも書いてあるでしょうというか，経済学の分野では，とにかく，「元の変数の対数をとって，重回帰...」とか書いてあるのでしょうが，原理についても勉強しましょう。

> 被説明変数に自然対数をとらないで，説明変数のみ取ればよいということなのですか

モデルが上のようならば，そんな変なことはしない。できない。してはいけない。

余計なことを考えるより，「非線形回帰」について，調べるほうが稔りがあるでしょう。

しかし，当てはめるべきモデルが上記のものでないのに，やみくもに（無批判に）対数をとろうとして困っているのなら，無駄なことです。
真に，どのようなモデルに当てはめるべきか，もう一度考える必要があるでしょう。

No.20399　Re: 従属変数について　　【推計初心者】　2013/11/01(Fri) 22:47

>y = α * x^β * z^γ * … * ε
返事ありがとうございました，何度もすいません。
自分が使っているモデルは青木先生が書いたのと同じです。
しかし，自分は被説明変数がマイナスということで今困っているのです。
ちなみに，自分がやろうとしている研究はオフショアリングが生産性（TFP）に与える影響についてです。先行研究のモデルを参考にしています。

一応自分はパネルで推計を行っているのですが，非線形回帰だと自然対数を取ったモデルと推計方法は同じでしょうか？

No.20400　Re: 従属変数について　　【青木繁伸】　2013/11/01(Fri) 23:42

> 自分は被説明変数がマイナスということで今困っているのです。

だから，非線形回帰を行ったらどうかと提案しているのです。
そもそも，対数をとって重回帰というのは，旧式のやり方だと書きました。

マイナスといってもどの程度のオーダーのマイナスなのか。
そもそも，y = α * x^β * z^γ * … * ε というモデルが成り立ち，α＞0 なら， y は負になりえないでしょう？わずかにマイナスということなら誤差としてたまたまそういうデータも観察されたと解釈できるのでしょうけど，絶対値が大きい負の値があるとなると，あなたのデータは，絶対にそのモデルには従わないということでしょう。

> 非線形回帰だと自然対数を取ったモデルと推計方法は同じでしょうか？

推計方法は違うでしょう。
対数をとるというのは，対数をとったデータについて（線形）最小二乗法
対数をとらずに，もとのままのデータをつかうのは非線形最小二乗法
答えは同じではない。しかし，違いの大きさは問題になる場合もならない場合もある。

No.20401　Re: 従属変数について　　【推計初心者】　2013/11/01(Fri) 23:59

> マイナスといってもどの程度のオーダーのマイナスなのか。
一応大きくても-0.1の数値です。

もうひとつ青木先生に質問を聞きたいのですが，
もし，先生が推計を行う時，被説明変数のデータにマイナスのデータがあったらどう対処するのでしょうか？
あと被説明変数のマイナスのデータは欠損値として扱うことはできますか？

No.20402　Re: 従属変数について　　【青木繁伸】　2013/11/02(Sat) 00:00

以下のような，従属変数が負になるデータでも，非線形最小二乗法ならば，あてはめできる。

> d # テストデータ（y が負のものがある）
    x          y
1   0  -5.000000
2   1  -3.000000
3   2   8.485281
4   3  15.588457
5   4  24.000000
6   5  33.541020
7   6  44.090815
8   7  55.560778
9   8  67.882251
10  9  81.000000
11 10  94.868330
12 11 109.448618
13 12 124.707658
14 13 140.616500
15 14 157.149610

y = 3*x^1.5 により作成。ただし，x=0,1 のときの y を -5, -3 に書き換えたもの

非線形最小二乗法によりあてはめ
> ans <- nls(y~a*x^b, d, start=list(a=2, b=2))
> summary(ans)

Formula: y ~ a * x^b

Parameters:
  Estimate Std. Error t value Pr(>|t|)
a  2.94904    0.19849   14.86 1.55e-09
b  1.50700    0.02763   54.55  < 2e-16

Residual standard error: 2.161 on 13 degrees of freedom

Number of iterations to convergence: 5 
Achieved convergence tolerance: 2.742e-06

推定されたパラメータによる予測値
> d2 <- list(x=seq(0, 14, by=0.1))
> pred <- predict(ans, d2)

図に描いてみる
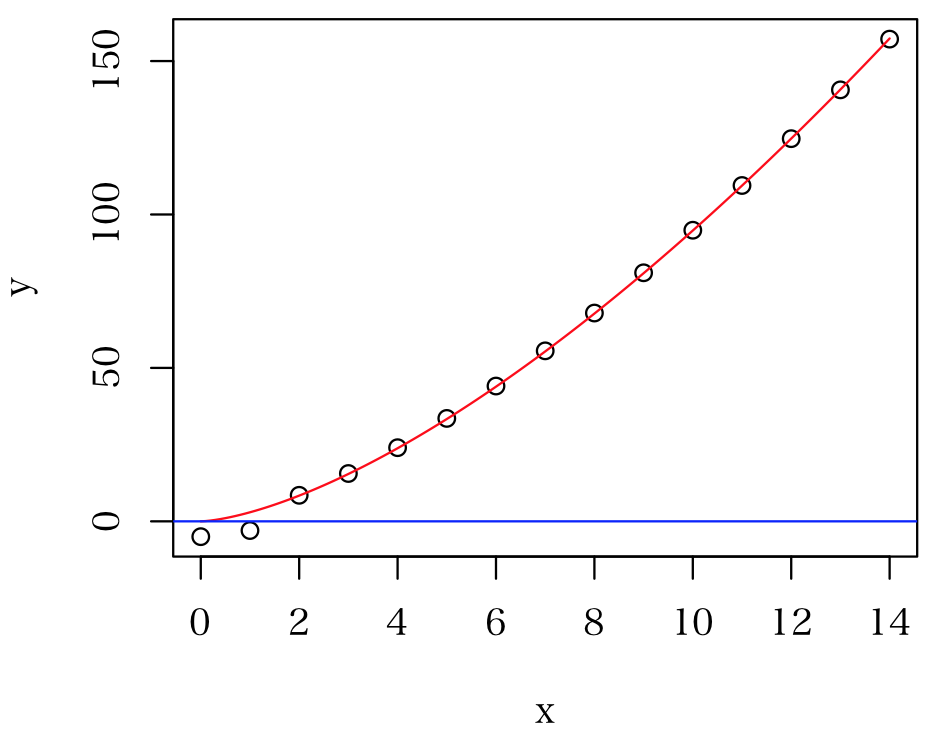
> plot(d)
> lines(d2$x, pred, col=2)
> abline(h=0, col=4)

○が，観測データ。赤は推定されたパラメータで描いた指数曲線。青はx軸（y=0）

No.20403　Re: 従属変数について　　【青木繁伸】　2013/11/02(Sat) 00:03

> 先生が推計を行う時，被説明変数のデータにマイナスのデータがあったらどう対処するのでしょうか？

何回もいっているように，非線形回帰を行う。非線形回帰なら，対数を採る必要がないのだから。

> あと被説明変数のマイナスのデータは欠損値として扱うことはできますか？

欠損値として扱いたければ，そのようにすればよい。

しかし，何度も言うが，非線形回帰を行えば良いだけだろう。くどい。
非線形回帰を知らないというなら，まずそれを知るべき。

No.20404　Re: 従属変数について　　【推計初心者】　2013/11/02(Sat) 00:13

わかりました。長く親切に付き合っていただいてありがとうございました。
非線形回帰を調べてみます。