「統計学関連なんでもあり」の過去ログ--- 046

No.20865　変数をケースにして平均を検定　　【Mac】　2014/02/11(Tue) 23:55

項目ごとに事前と事後の回答を記録し，以下のように集計したものをさらにウィルコクソンの符号付順位和検定で分析するという方法は，「事前と事後の変化を検討する」という目的で使用できるのでしょうか？（実際には被験者8人，項目がバラバラの刺激の9項目です。）

項目　　事前　事後
項目1　2.63　2.13
項目2　2.63　3.00
項目3　2.88　2.25
項目4　3.63　2.13
項目5　2.25　2.50
平均　 2.80　2.40

項目ごとに同じ被験者からの回答が含まれているので，データの独立性が保たれておらず，検定するのは適切ではないと思ったのですが，いろいろ調べてみても正しいか間違っているかどうかがわからなかったので，ご教授いただければ助かります。どうぞよろしくお願いいたします。

No.20872　Re: 変数をケースにして平均を検定　　【斜界人】　2014/02/12(Wed) 22:40

> 検定するのは適切ではないと思った
多分そのとおりだと思います。
平均を求めたということは間隔尺度以上として扱えるのでしょうか。それならば被験者内計画の二要因分散分析ですが...ちょっと強引かもしれませんね。

No.20881　変数をケースにして平均を検定　　【Mac】　2014/02/14(Fri) 21:49

斜界人様，ご意見どうもありがとうございました。

No.20882　変数をケースにして平均を検定　　【Mac】　2014/02/17(Mon) 10:13

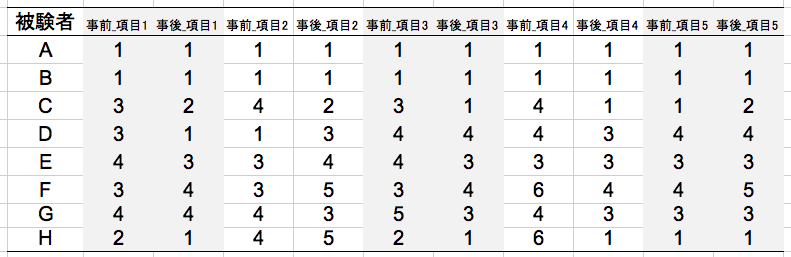
すみません。この件に関連してなのですが，統計的検定に用いるデータは，通常，サンプル（人など）がケースになって，項目や刺激が変数になりますよね。

例えば，被験者の能力を推定する場合には person ability になりますが，項目や刺激の側から整理すると，item difficulty ととらえられるので，itemとperson はまったくのミラーイメージとなり，同じ項目群を2回やった被験者群のスコアを検定する（＝同じ母集団からきた被験者群とみなせるか）のが可であれば，まったく同様に，同じ被験者群に2回試行された項目群の成績を検定する（＝同じ母集団からきた項目群とみなせるか）も可となるように思えます。

そういうデータを転置して，項目や刺激をケースとし，サンプル（人など）を変数として検定するような方法は，そもそも可能なのでしょうか？

No.20883　Re: 変数をケースにして平均を検定　　【斜界人】　2014/02/17(Mon) 19:11

この場合，反応変数は回答で，説明変数は被験者，項目，時間（事前事後）とするより仕方ないのでは。

被験者を反応変数とみなすなら，回答がk段階あるとして，9項目あるからk^9通りの値を取りうることになります。
項目を反応変数とみなすなら同様にしてk^8とおりの多値です。
反応変数は名義尺度としてしか扱えなくなります。更に事前事後は対応ありです。
比較するのは無理でしょう。

分割表は，同一対象からの情報はただひとつのセルに現れるようにするのが原則です。項目1だけを取り上げてみると，回答は6段階として，6x6の2次元
    事後
事前 1 2 3 4 5 6
   1 2 0 0 0 0 0
   2 1 0 0 0 0 0
   3 1 1 0 1 0 0
   4 0 0 1 1 0 0
   5 0 0 0 0 0 0
   6 0 0 0 0 0 0
となります。被験者Aの回答は（事前=1, 事後=1）なので，(1,1)のセルにただ一度だけカウントされます。同様に被験者Cは(3,2)のセルに入ります。これだと期待度数が低すぎてカイ二乗近似は使えません。
実際にはk^9xk^9の二次元分割表です。あるいは，被験者の属性を（項目1.事前，項目1.事後，項目2.事前，...，項目9.事後）として，18元クロス集計です。多元集計だと分析法があるのかどうか知りませんが，どっちにしても莫大な数の被験者が必要になるでしょう。

そこで回答を間隔尺度とみなして，項目ごとに符号付順位和検定（全体は諦める），あるいは被験者内計画二要因分散分析などが考えられますが，無理矢理な感じではあります。

No.20884　Re: 変数をケースにして平均を検定　　【青木繁伸】　2014/02/17(Mon) 19:58

根本的な考え方です。
観察の単位はひとつひとつの測定値ということ。いくつかの測定値を，平均したり，中央値を取ったり，その他いろんな規則（規則とも言えない手続き）で（むりやり）一つにしたものではないということ。
同じサンプルが1回限り観察されるなら独立なデータ。
同じサンプルが繰り返し観察されるなら対応のあるデータ。
観察される変数が複数あるなら，変数ごとに独立であったり，対応があったり。
観察されたデータを何らかの方法でまとめたものをサンプルと見なして統計処理を行うというのは，たいていは誤り。たとえば，独立なサンプルで二変数を観察するときに，サンプルごとに観察回数が違うとき，サンプルごとに変数の平均値2個を元にして相関係数を計算するようなこと。観察回数がサンプルごとに異なるような場合，この方法が不適切なのは明らか。
統計解析・検定手法というのはあらゆる状況の下で得られるデータに対応しているわけではない。条件を満たしていないデータは分析も検定も出来ないだろうということ。

分かりやすいのは，「検定というのはサンプルサイズに依存する」という大原則。
何らかの形でデータをまとめるというのは，「もともとのサンプルサイズによらず，算出された数値の【サンプルサイズは1とする】」という暗黙の手続き。たとえば，Aさんの5回の血圧値の平均値を1つの「最高血圧/最低血圧」とするということ。このようなことがなされるならば，Bさんの10000回の血圧値の平均値を1つの「最高血圧/最低血圧」としたものと同じように比較することは出来ないだろうということ。

データ行列として考えればよく分かるだろう。
一行は一つの観察
一つの観察には，複数の変数がある。
その変数の中には，そのデータがある個人の特定の条件下の測定値であるという指標もある。
そのような状況では，ある一個人のデータは複数行を占める。
逆に言えば，どの行がある個人のどのような条件下のデータであるかが分からないといけないということ。
複数の行が，別々の個人のデータなのか，同じ個人のデータなのか識別できないようでは，どんな分析もできない。

「データさえ取っておけば何とかなるだろう」
「1回だけ測定するより，複数回測定した方が正確だろう」
それが正しい場合もあるだろうし，余計なことをしたから分析方法が見つからない？？ということもあるかも知れない？？

No.20886　変数をケースにして平均を検定　　【Mac】　2014/02/18(Tue) 14:59

斜界人様，青木先生，詳しいご意見をいただきどうもありがとうございました。
サンプルと変数を転置してまとめ，検定するような方法は正しくないということを理解しました。